A Standard Set by SEBI for PMS Fund Managers

Measuring the return is the most integral part of any investment portfolio. Although it seems like a simple calculation, it isn’t exactly the case. There is more than one way of measuring the return on an investment portfolio, and in many situations, the results will differ depending on the methodology we choose.

This might seem confusing but read on to clear up this confusion. And let’s understand which approach best suits the investment situation.

What it is?

The time-weighted rate of return (TWRR) measures the compound growth rate in a portfolio over a specified period. When there are multiple transactions in the investment portfolio during the investment tenure, it may not depict the correct picture to average out the peaks and troughs and look at the rate of return. This is where the time-weighted rate of return comes to the rescue.

The TWRR measure is often used to compare the returns of investment portfolios because it divides the return on a portfolio into separate sub-periods or intervals based on the investments and redemptions made and eliminates the distorting effects of growth rates created by cash inflows and outflows.

The TWRR is calculated by breaking up the investment period into smaller chunks based on the inflows and outflows in the investment account. Each time there is a deposit or withdrawal from the investment account, it marks the end of one period and the start of another.

While calculating TWRR, one looks at how the investments performed in each period and then combines the results.

Let’s understand it better with an example:

In this example, we’ll consider two time periods, but depending on your cash flows, there could be multiple periods to consider than this.

E.g., Mr X invested ₹ 10,00,000 in Portfolio A on 31st Dec 2020. By 1st Sep 2021, his portfolio has grown to ₹ 10,53,418. He then makes an additional investment of ₹ 1,00,000 in the investment account for a total value of ₹ 11,53,418. At the end of 31st Dec 2021, the portfolio value decreased to ₹ 10,75,816.

Now let’s calculate the first-period return:

(₹ 10,53,418 – ₹ 10,00,000) / ₹ 10,00,000 = 5.34%

The second-period return would be:

[₹ 10,75,816 – (₹ 10,53,418 + ₹ 1,00,000)] / (₹ 10,53,418 + ₹ 1,00,000) = -6.72%

Finally, to calculate the TWRR, we’ll multiply each sub-period rate of return together:

TWRR = [(1+5.34%) x (1-6.73%)] – 1 = -1.74%

In the example above, you can see that your time-weighted rate of return is -1.74% over 12 months.

Two practical methods for measuring the performance

The practical methods of evaluating investment performance are the Time Weighted Rate of Return (TWRR) and Money Weighted Rate of Return (MWRR). The only difference between these two methods is how they treat the cash in-flows and outflows in an investment portfolio.

The TWRR measure eliminates these cash flows from the calculation, whereas MWRR considers it while computing the rate of return.

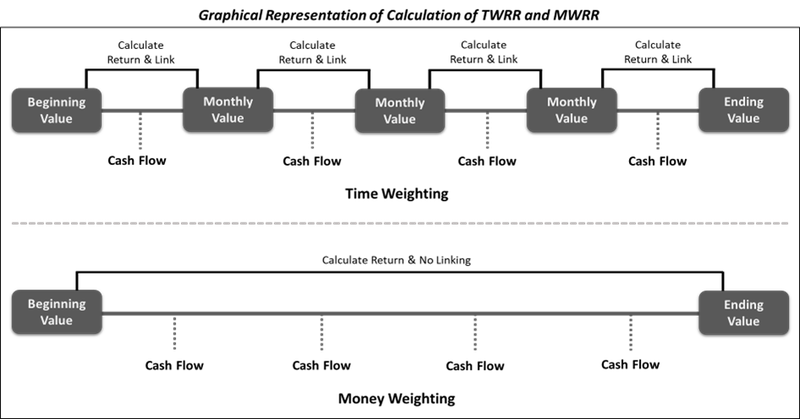
TWRR & MWRR - A practical example

Let’s consider a PMS (Portfolio Management Service) firm how is managing funds for three different clients and evaluate the results from TWRR and MWRR.

Both TWRR & MWRR have provided helpful information – the TWRR shows how well the underlying investment decisions have performed, and the MWRR shows how well the actual money invested in the portfolio did, the difference being the impact of cash inflows and outflows at times.

The above paragraph explains why TWRR is vital for performance calculation. Earlier, fund managers used multiple methods at their convenience to calculate the returns of their strategies, which created a lot of confusion.

Finally, in 2020 PMS regulations, SEBI mandated PMS providers to use TWRR as a standard measure to calculate performance for each strategy. TWRR eliminates the client-led cash flows from the portfolio and calculates all returns in an investment approach. This approach requires aggregating portfolios with a similar asset class or strategy and calculating returns